Graph Theory
For a simple graph G, prove that G is a cycle iff every vertex has degree 2.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 HomeworkSolutionNecessary condition: If $G$ is a cycle, then every vertex in $G$ has degree 2.(a). A cycle is a simple path that starts and ends at the same vertex. Every vertex is visited exactly once.(b). In a cycle, each vertex is connected to exactly two other vertices: one edge connects to the previous vertex in the cycle, and one edge co..
Use induction to prove that if a graph does not have an odd cycle thenit is bipartite. , Comment: You should first choose which parameter thatyou will apply induction on - number of vertices or number of edges.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2SolutionP(n): A graph with $n$ vertices and no odd cycles is bipartite.(i). Base step:- For $n = 1$, a graph with a single vertex is trivially bipartite.- For $n = 2$, a graph with two vertices cannot have an odd cycle and is bipartite.(ii). Inductive hypothesis:Assume $P(k)$ is true for some positive integer $k$.That is, any graph w..
Prove that the Petersen graph has no cycle of length 7.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework2Solution(i). Assume that the Petersen graph has a cycle of length 7. Call this cycle ( C_7 ).(ii). Each vertex in ( C_7 ) has two edges within the cycle. Since the Petersen graph is 3-regular, each vertex must have one additional edge connecting to a vertex outside of the cycle.(iii). This additional edge cannot connect to another ver..
![Identify the vertices of a Petersen graph in your drawing and explainwhy. (Note again that the vertex set of the Petersen graph is the collec-tion of 2-subsets of [5], for example, 13 means {1, 3}. Two vertices aband cd are adjacent iff {a, b} ∩ {c, d} =∅](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4shDt%2FbtsLzXqc85i%2FSJox0MbB57pHyR66VAshgK%2Fimg.png)
Identify the vertices of a Petersen graph in your drawing and explainwhy. (Note again that the vertex set of the Petersen graph is the collec-tion of 2-subsets of [5], for example, 13 means {1, 3}. Two vertices aband cd are adjacent iff {a, b} ∩ {c, d} =∅
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2SolutionThe set ([5] = \{1, 2, 3, 4, 5\}) has the following 2-subsets:[12, 13, 14, 15, 23, 24, 25, 34, 35, 45.]These 10 subsets form the 10 vertices of the Peterson graph.To determine adjacency, the rule is:Two vertices (ab) and (cd) are adjacent if and only if (\{a, b\} \cap \{c, d\} =∅).Example:Vertex (34) is adjacent to (12), (25)..
Let Gn be the simple graph with vertex set v0, v1, · · · , vn−1 such that viand vj are adjacent if and only if |j − i| ∈ {4, 5}. Draw the graphs G5 andG6. Determine the number of components of Gn.
문제출처- 광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2Solution(i). G_{5}(ii). G_{6}Number of connected components in $G_{n}$ is$$\begin{cases}n, & \text{if } 0 \leq n \leq 4, \\9 - n, & \text{if } 5 \leq n \leq 8, \\1, & \text{if } n \geq 9.\end{cases}$$
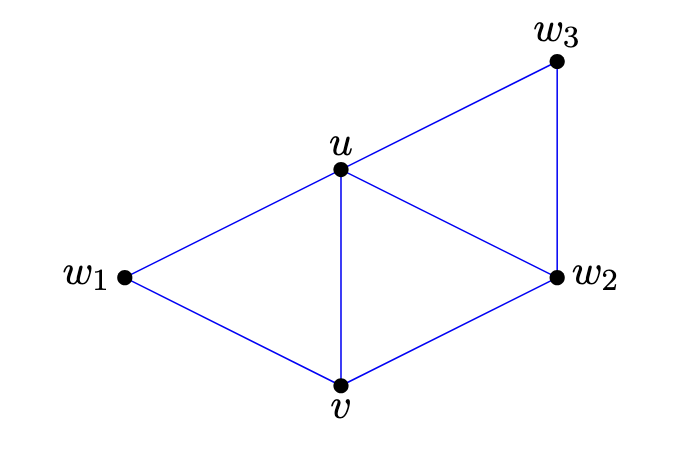
Let u and v be adjacent vertices in a simple graph G. Prove that uvbelongs to at least $$ d(u) + d(v) - n(G) $$ triangles in G.
문제출처 - 광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2Solution(i). Since $u$ and $v$ are adjacent, $uv$ is an edge in $G$.(ii). The number of triangles containing $uv$ is the same as the size of the intersection of $N(u)$ and $N(v)$. $N$ means neighbor.(iii). For example, if $N(u) = \{v, w_1, w_2, w_3\}$ and $N(v) = \{u, w_1, w_2\}$, then:$$N(u) \cap N(v) = \{w_1, w_2\}.$$Thus, the t..