그래프이론

Graph Theory
Let G be a simple graph of even order n having a set S of size k such that o(G-S) > k. Prove that G has at most $\binom{k}{2} + k(n-k) + \binom{n-2k-1}{2}$ edges, and that this bound is best possible. Use this to determine the maximum size of a simple $n$
문제출처광주과학기술원 GIST 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 7Solution1. The total number of edges in $G$ can be expressed as: $$|E(G)| = e(G[S]) + |[S, \bar{S}]| + e(G[\bar{S}]),$$ where $e(G[S])$ is the number of edges within $S$, $|[S, \bar{S}]|$ is the number of edges between $S$ and $\bar{S}$, and $e(G[\bar{S}])$ is the number of edges within $\bar{S}$. 2. Since the size of $S$ i..
→2025.01.14
Graph Theory
Prove that the Petersen graph has no cycle of length 7.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework2Solution(i). Assume that the Petersen graph has a cycle of length 7. Call this cycle ( C_7 ).(ii). Each vertex in ( C_7 ) has two edges within the cycle. Since the Petersen graph is 3-regular, each vertex must have one additional edge connecting to a vertex outside of the cycle.(iii). This additional edge cannot connect to another ver..
→2024.12.28
Graph Theory
Identify the vertices of a Petersen graph in your drawing and explainwhy. (Note again that the vertex set of the Petersen graph is the collec-tion of 2-subsets of [5], for example, 13 means {1, 3}. Two vertices aband cd are adjacent iff {a, b} ∩ {c, d} =∅
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2SolutionThe set ([5] = \{1, 2, 3, 4, 5\}) has the following 2-subsets:[12, 13, 14, 15, 23, 24, 25, 34, 35, 45.]These 10 subsets form the 10 vertices of the Peterson graph.To determine adjacency, the rule is:Two vertices (ab) and (cd) are adjacent if and only if (\{a, b\} \cap \{c, d\} =∅).Example:Vertex (34) is adjacent to (12), (25)..
→2024.12.28
Graph Theory
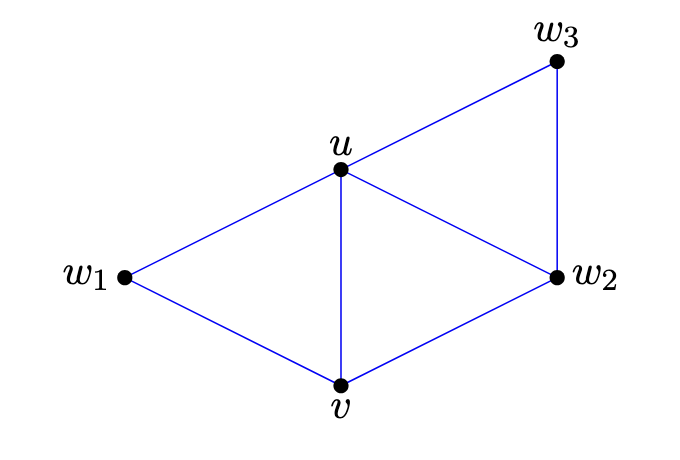
Let u and v be adjacent vertices in a simple graph G. Prove that uvbelongs to at least $$d(u) + d(v) - n(G)$$ triangles in G.
문제출처 - 광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2Solution(i). Since $u$ and $v$ are adjacent, $uv$ is an edge in $G$.(ii). The number of triangles containing $uv$ is the same as the size of the intersection of $N(u)$ and $N(v)$. $N$ means neighbor.(iii). For example, if $N(u) = \{v, w_1, w_2, w_3\}$ and $N(v) = \{u, w_1, w_2\}$, then: $$N(u) \cap N(v) = \{w_1, w_2\}.$$ Thus, the t..
→2024.12.28

• 이전
• 1
• 다음