
✏️ 문제
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net

✏️ 풀이
뭘 어쩔지 모를땐 늘 그렇듯 규칙을 찾아보자.
모든 경우의 수를 한번 생각해보았다.
n=1 > size 1 : 1개

n=2 > size 1: 2개 || size 2: 1개

n=3 > size 1: 3개 || size 1: 1개 + size 2: 2개 || size 1: 2개 + size 2: 1개

n=4 > size 1: 4개 || size 1: 2개 + size 2: 2개(L) || size 1: 2개 + size 2: 2개(R) || size 1: 1개 + size 2: 2개 + size 1: 1개
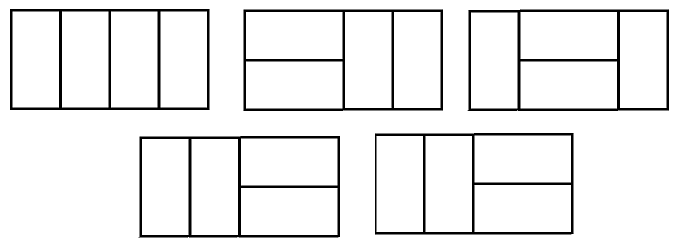
규칙이 보이지 않는가? 2xn 사이즈의 직사각형으로 채우려면 2x(n-1) 직사각형을 채우는 경우와 2x(n-2) 직사각형을 채우는 방법을 더하면 된다.
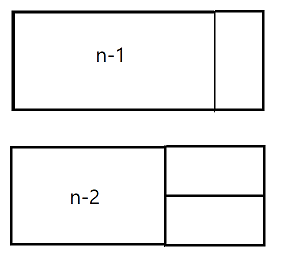
이미지는 아래 assb 님의 블로그에서 가져왔다.
백준 11726번: 2xn 타일링
https://www.acmicpc.net/problem/11726 11726번: 2×n 타일링 2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지..
assb.tistory.com
다이나믹 프로그래밍(Dynamic Programming)
위에서 2xn 사이즈의 직사각형으로 채우려면 2x(n-1) 직사각형을 채우는 경우와 2x(n-2) 직사각형을 채우는 방법을 더하면 된다고했다. 즉 2xn문제를 해결하기 위해 작은 문제들을 해결하면 된다는 뜻이다. 전형적인 동적계획법 문제이다.
다이나믹 프로그래밍에 대해서는 아래글을 참고하라.
[Python & Algorithm] Dynamic Programming(동적프로그래밍)
✏️ Dynamic Programming 큰 문제를 작은 문제로 나누어 푸는 문제를 이야기한다. 이름에 의미는 없다. 그냥 말이 멋있어서 이렇게 지었다고 한다. 1) 분할정복과의 차이 '작은 문제가 중복이 일어나
duckracoon.tistory.com
"2xn 사이즈의 직사각형으로 채우려면 2x(n-1) 직사각형을 채우는 경우와 2x(n-2) 직사각형을 채우는 방법을 더하면 된다." 라는 말이 잘 이해가지 않는다면 순열을 떠올려보자.
[1, 2, 3, 4]로 만들 수 있는 순열은 이와 같다. [1, 2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2], [1, 4, 2, 3], [1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3], .....
시작인 1인 순열의 수는 얼마나 될까? 1을 제외한 뒤 3개의 숫자 [2, 3, 4]로 순열을 만드는 경우의 수가 될 것이다. 즉 3! = 6
일반화하면 n개의 숫자로 순열을 만들 때 하나의 숫자 자리가 정해진다면 나머지로 만들어지는 순열의 경우는 (n-1)!이다. 정해진 자리가 2개라면 (n-2)!이다. 2xn 타일링 문제도 이와 같다. 그럼 왜 2x(n-3) 직사각형을 채우는 방법은 더하지 않나? 왜 cache[n]=cache[n-1]+cache[n-2]로 접근해야하는걸까? cache[n-3]은 cache[n-1], cache[n-2]로 표현가능하기 때문이다.
(Python)
n = int(input())
# memoization을 위함
cache = [0]*1001
# n이 1,2인 경우는 명확하니까 미리 선언해둔다.
cache[1]=1
cache[2]=2
# dynamic programming
for i in range(3,1001):
cache[i] = (cache[i-1]+cache[i-2])%10007
print(cache[n])
'프로그래밍 > 백준' 카테고리의 다른 글
| 백준 2579: 계단오르기 해설- python (0) | 2022.01.30 |
|---|---|
| 백준 2748번 런타임에러(IndexError) (0) | 2022.01.27 |
| 백준 9095: 1, 2, 3 더하기 해설- python (0) | 2022.01.26 |
| 백준 11727: 2xn 타일링(2) 해설- python (0) | 2022.01.23 |
| 백준 1463: 1로 만들기 해설- python (0) | 2022.01.23 |
