
✏️ Dynamic Programming
큰 문제를 작은 문제로 나누어 푸는 문제를 이야기한다. 이름에 의미는 없다. 그냥 말이 멋있어서 이렇게 지었다고 한다.
1) 분할정복과의 차이
'작은 문제가 중복이 일어나는지 아닌지' 에 차이가 있다. 분할정복은 큰 문제를 해결하기 어려워서 단지 작은 문제로 나누어서 푸는 방법이다. 특징은 작은 문제에서 반복이 일어나는 부분이 없다는 점이다. 하지만 동적프로그래밍은 작은 부분문제들이 반복되는 것을 이용해 문제를 풀어낸다.
2) 다이나믹 프로그래밍의 방법
모든 작은 문제들은 한번만 풀어낸다. 따라서 정답을 구한 작은 문제를 어딘가에 메모해둔다. 다시 그보다 큰 문제를 풀어나갈 때 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제의 결과값을 이용한다.
3) 다이나믹 프로그래밍의 사용조건
- 작은 문제가 반복이 일어날 때
- 같은 문제는 구할때마다 답이 같다
4) Memoization (메모이제이션)
한번 계산한 작은 문제들을 저장해놓고 다시 사용한다고 했다. 이것을 메모이제이션이라고 한다.
피보나치 연산을 예로 들어보자.
def fib(n):
if n < 0:
raise IndexError(
'Index was negative.'
'No such thing as a negative index in a series.'
)
elif n in [0, 1]:
# Base cases
return n
print("computing fib(%i)" % n)
return fib(n - 1) + fib(n - 2)위는 n번째 피보나치 수를 계산하는 재귀식이다. 이는 같은 입력값에 대해 여러번의 실행을 발생시킨다.

n이 증가함에 따라 호출되는 함수의 수가 기하급수적으로 증가하게 될 것이 보이는가. 덧셈연산이 2^0+2^1+2^2+...+2^(n-4)+2^(n-3)번 이루어지고 즉 2^(n-2)-1번 이루어진다. 시간복잡도는 O(2^n)으로 나타나고 n의 개수가 50만 되어도 2^50=1,125,899,906,842,624번 연산을 해야한다.
def memo_fibo(n):
memo[0] = 1
memo[1] = 1
if n<2:
return memo[n]
for i in range(2, n+1):
memo[i] = memo[i-2] + memo[i-1]
return memo[n]
if __name__ == '__main__':
n = int(sys.stdin.readline())
memo = [0 for i in range(n+2)]
print(memo_fibo(n))
print(memo)위는 동적프로그래밍으로 구현된 코드다. 0,1번째 수열은 항상 1이므로 배열에 미리 저장하고 2번째 수열을 구할때는 배열(memo)에 저장된 값을 이용한다(memoization). 구한 2번째 수열의 결과값을 배열에 다시 저장한다. 그런식으로 진행하며 입력받은 n 번째 수열을 구하게 된다.
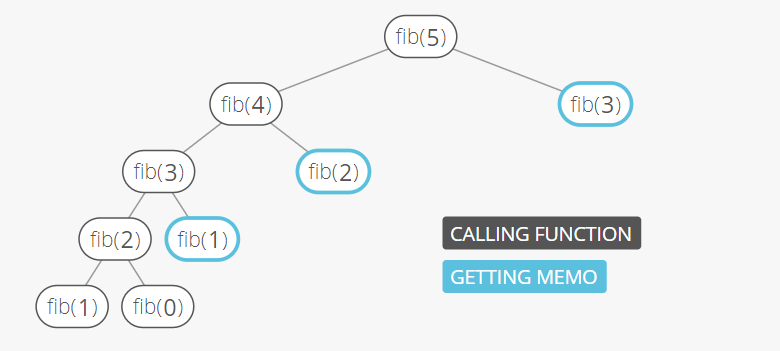
더 이상 반복되는 노드가 없다.
[2022.01.26 추가 헛소리]
DP공부중인데 조금 안풀리면 풀이만 찾아 헤매고있다. 반성하며 고민하는 시간을 늘리려 노력하려한다. 근무서고 당직서면서도 계속 풀이를 고민해봐야겠다. DP에 있어 풀이를 보는 건 독이다. 느끼고 있다.
'프로그래밍 > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘] Lower Bound와 Upper Bound (1) | 2022.02.02 |
|---|---|
| Binary Search (이진탐색) 알고리즘 (0) | 2022.02.01 |
| [Python & Data Structure] Graph (0) | 2021.11.04 |
| [Python & Data Structure] Tree (0) | 2021.11.02 |
| [Python & Data Structure] Queue, Stack, Linked List (1) | 2021.11.01 |
![[Python & Algorithm] Dynamic Programming(동적프로그래밍)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FCOwER%2FbtrrpT1LhQE%2FFZvGVxtmqQdonWjMmTMkR1%2Fimg.jpg)