
✏️ Graph (그래프의 개념)
- 연결되어 있는 객체간의 관계를 표현하는 비선형 자료구조
- 가장 일반적인 자료구조의 형태이며, Tree 도 그래프의 특수한 경우이다.
- 하나의 점을 Vertex 라고 한다.
- 하나의 선을 Edge 라고 한다. Link 라고도 함.

✏️ Graph (용어)
- 비가중치 그래프 / 가중치 그래프
: 비가중치 그래프는 각 vertex 간의 연결 유무만을 판단한다. 가중치 그래프는 각 간선(edge)에 가중치를 부여한 형태로 예를 들면 edge에 비용을 부과하는 형식으로 가중치가 부과될 수 있다. 위의 그림은 가중치 그래프이다.
- 무향(undirected) 그래프 / 유향(directed) 그래프
: 무향 edge는 양방향의 의미를 가진다. (A,B)=(B,A) 로 순서에 의미를 가지지 않는다. 방향 그래프는 edge를 통해서 한 방향으로만 갈 수 있다. <A,B> =/= <B,A> .

- 인접(adjacency) 정점
: 한 vertex에서 edge로 직접 연결된 vertex. '그래프의 개념'에서 이용한 그래프를 참고한다면 vertex 4 의 인접정점은 vertex 3 이다.
- 그래프의 차수(degree)
1) 무향 그래프 : 그래프의 차수는 인접 정점의 수와 같다. 따라서 모든 차수의 합은 edge 개수의 2배라는 특성을 가진다.
2) 유향 그래프 : 집입차수 (in-degree) 와 진출차수 (out-degree)로 구분된다. 진입차수는 외부에서 오는 간선의 수이며, 진출 차수는 외부로 향하는 간선의 수이다. 방향 그래프의 모든 진입차수 또는 진출차수의 합은 에지의 수와 같다. 즉, 진입차수의 합 = 진출차수의 합 = 그래프 내 모든 간선의 수.
✏️ Graph (용어)
- 비가중치 그래프 / 가중치 그래프
: 비가중치 그래프는 각 vertex 간의 연결 유무만을 판단한다. 가중치 그래프는 각 간선(edge)에 가중치를 부여한 형태로 예를 들면 edge에 비용을 부과하는 형식으로 가중치가 부과될 수 있다. 위의 그림은 가중치 그래프이다.
- 무향(undirected) 그래프 / 유향(directed) 그래프
: 무향 edge는 양방향의 의미를 가진다. (A,B)=(B,A) 로 순서에 의미를 가지지 않는다. 방향 그래프는 edge를 통해서 한 방향으로만 갈 수 있다. <A,B> =/= <B,A> .

- 인접(adjacency) 정점
: 한 vertex에서 edge로 직접 연결된 vertex. '그래프의 개념'에서 이용한 그래프를 참고한다면 vertex 4 의 인접정점은 vertex 3 이다.
- 그래프의 차수(degree)
1) 무향 그래프 : 그래프의 차수는 인접 정점의 수와 같다. 따라서 모든 차수의 합은 edge 개수의 2배라는 특성을 가진다.
2) 유향 그래프 : 집입차수 (in-degree) 와 진출차수 (out-degree)로 구분된다. 진입차수는 외부에서 오는 간선의 수이며, 진출 차수는 외부로 향하는 간선의 수이다. 방향 그래프의 모든 진입차수 또는 진출차수의 합은 에지의 수와 같다. 즉, 진입차수의 합 = 진출차수의 합 = 그래프 내 모든 간선의 수.
- 자기루프 (self loop)
정점에서 출발한 간선이 바로 자기자신에게 진입하는 경우. 다른 정점을 거치지 않는다.
- 사이클 (cycle)
한 정점에서 출발해 다시 해당 정점으로 돌아갈 수 있는 경우.
✏️ Graph의 표현 : 인접행렬과 인접리스트
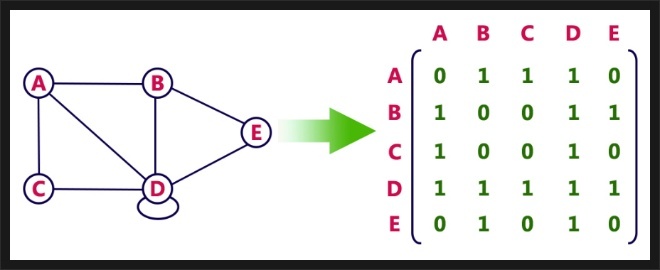
인접행렬
- 만약 A라는 점과 B라는 정점이 연결되어있다면 1, 아니면 0으로 표시한 행렬
- 만약 가중치 그래프라면 1 대신 가중치를 저장한다.
- 최단경로문제에서 주로 사용된다
[Sudo code]
for i in range(n_row)
for j in range(n_row)
if (edge exists):
A[i][j] = 1
else:
A[i][j] = 0* self loop가 없다면 단순그래프의 인접행렬의 대각성 성분은 모두 0 이 된다. 또한 무향 그래프의 인접행렬은 대칭 행렬이다.
인접리스트
- 인접리스트는 각 vertex가 어떤 정점과 인접한지를 리스트의 형태로 표현한 것이다.
- 각 정점마다 하나의 리스트를 가진다.
- 하나의 리스트는 자신과 인접한 다른 정점을 담고 있다.

간단한 구조의 그래프는 인접행렬로 구현이 가능하지만 시간복잡도 O(n^2)가 걸리기 때문에 그래프의 vertex가 많다면 O(n)이 걸리는 인접리스트로 구현하는 것이 효율적이다. 복잡하고 어려운 상황의 그래프에서는 인접리스트가 더 효율적으로 그래프를 저장, 탐색하도록 해준다.
[파이썬에서 인접리스트의 구현]
파이썬은 포인터가 따로 존재하지 않는다. 따라서 출발노드를 키로, 도착노드를 값으로 표현하는 딕셔너리 형태로 표현한다.
G = {
0: [1],
1: [0, 2],
2: []
}
DFS와 BFS 까지 설명하고 구현하려했는데 따로 쓰는게 좋을 것 같아서 다음 글에 이어서 작성하려한다.
'프로그래밍 > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘] Lower Bound와 Upper Bound (1) | 2022.02.02 |
|---|---|
| Binary Search (이진탐색) 알고리즘 (0) | 2022.02.01 |
| [Python & Algorithm] Dynamic Programming(동적프로그래밍) (0) | 2022.01.22 |
| [Python & Data Structure] Tree (0) | 2021.11.02 |
| [Python & Data Structure] Queue, Stack, Linked List (1) | 2021.11.01 |
![[Python & Data Structure] Graph](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FxDtKr%2FbtrjUThGCJz%2FAAAAAAAAAAAAAAAAAAAAAJB63IeowD0n31n8C6U4JiA1Vp2k6nT9Om2kkvD4x2sN%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DfudPY%252BgJMFqE6lrT6QykoEFwkNg%253D)