* 잘못된 내용이 있다면 댓글로 바로잡아주시면 감사드리겠습니다

✏️ Tree (트리의 개념)
리스트나 스택, 큐로 가계도나 조직도를 구현할 수 있을까? 선형자료구조로는 계층형 구조를 표현하기 어렵다. 계층형 구조를 가진 문제를 해결하기 위한 자료구조가 '트리'이다.
- 무방향 그래프의 한 구조
- 하나의 데이터 뒤에 여러개의 데이터가 존재할 수 있는 비선형 구조이다.
- 계층적으로 표현되며 아래로만 뻗어나가기에 사이클이 없다
- 루트라는 하나의 꼭짓점 데이터를 시작으로 여러개의 데이터를 간선으로 연결한다.
- 트리구조는 각 데이터를 노드라고 하며, 두개의 노드가 상하계층으로 연결되면 부모/자식 관계를 가진다.
- 자식이 없는 노드는 leaf node라고 부른다
- Tree는 깊이와 높이, 레벨등을 측정할 수 있다.
✏️ Tree (용어)
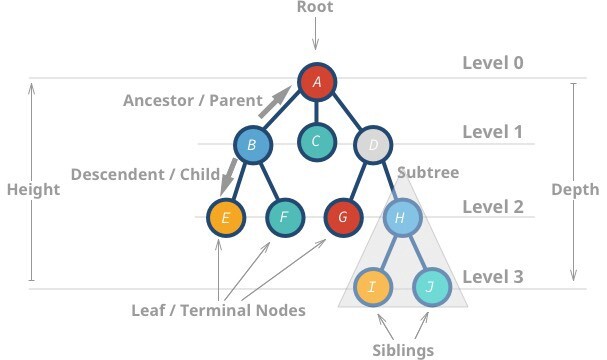
Node
- 트리구조를 이루는 모든 개별 데이터
Root
- 트리구조의 시작점이 되는 노드
Parent node
- 부모노드란 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 가까운 노드
Child node
- 자식노드란 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 먼 노드
Leaf
- 트리구조의 끝 지점이며, 자식노드가 없는 노드
Depth
- 루트로부터 하위계층의 특정노드까지의 depth를 표현할 수가 있다
- 루트는 depth(깊이)가 0이다.
- 루트에서 어떤 노드에 도달하기위해 거쳐야하는 간선의 개수
- E의 depth는 2, I에서의 depth는 3
Level
- 트리에서 같은 depth를 가지는 노드를 묶어서 Level로 표현할 수 있다.
- 루트노드를 레벨 0으로 두는 사람도 있는 것 같고, 레벨 1로 두는 사람도 있는 것 같다.
- 같은 레벨에 나란히 있는 노드를 sibiling Node라고 한다.
Height
- 리프노드의 높이를 0으로 둔다.
- 트리의 높이는 루트노드에서 가장 깊이 있는 노드의 깊이(leaf의 깊이?) 로 볼 수 있을 것.
Sub tree
- 큰 트리의 내부에서 트리구조를 갖춘 작은 트리를 말한다.
✏️ Tree (기본적인 성질)
- 노드가 N 개인 트리는 항상 N-1 개의 링크를 가진다.
- 트리에서 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드간의 경로도 유일하다.
✏️ Tree의 종류
5가지 정도만 정리한다.
1) 이진트리 (Binary Tree)

노드가 하나이상의 자식을 가지게 되면 트리라고 위에서 정의했다. 자식노드를 최대 2개까지만 허용하는 트리를 이진트리라고 부른다.
이진트리의 순회는 재귀호출을 사용한다. 따라서 전위, 중위, 후위 순회를 간단하게 구현할 수 있다. 순회란 모든 원소를 빠지거나 중복하지핞고 처리하는 연산을 의미한다.
* 완전이진트리(Complete Binary Tree)
노드 삽입시 왼쪽부터 차례로 채워나간 트리이다.


* 전위(preorder), 중위(inorder), 후위(postorder) 순회
preorder traverse : root를 먼저 방문
inorder traverse: 왼쪽 하위 트리를 방문 후 root를 방문
postorder traverse: 하위트리를 모두 방문 후 root를 방문

전위 순회 : 0->1->3->7->8->4->9->10->2->5->11->6
중위 순회 : 7->3->8->1->9->4->10->0->11->5->2->6
후위 순회 : 7->8->3->9->10->4->1->11->5->6->2->0
2) 스레드 이진트리 (Threaded Binary Tree)
이진트리는 재귀호출을 사용한다고 헀다. 하지만 재귀호출은 반복문에 의해 비효율적이며 이 비효율성은 트리의 높이가 커질 수록, 노드의 개수가 많아질수록 더 커지게 된다. 스레드 이진트리는 재귀호출없이 순회할 수 있도록 구현된 트리이다.
3) 이진탐색트리 (Binary Search Tree)
이진트리는 자식노드를 최대 2개 허용한다고 했다. 이진탐색트리는 조건이 더 붙는다. 왼쪽 노드와 그 이하의 자식노드들이 현재의 노드보다 작아야하며 오른쪽 노드와 그 이하의 자식들은 현재의 노드보다 커야한다. 그러므로 모든 값들이 노드들을 기준으로 두가지 방향으로 찾으면 되기에 값을 찾는데 편리한 조건을 가지고 있다.
4) AVL 트리
AVL 트리는 스스로 균형을 잡는 이진트리이다. 트리의 높이가 h일때 이진탐색트리의 시간복잡도는 O(h) 가 되며 한쪽으로 치우친 편향된 이진트리가 되면 트리의 높이가 높아지고 즉 시간복잡도가 높아진다. 이를 방지하기위해 높이 균형을 유지하는 AVL트리를 사용하게 된다.
5) 히프
최대값과 최솟값을 찾아내는 연산을 하기위한 완전이진트리를 기본으로 한 자료구조이며 부모노드의 키 값이 자식노드의 키값보다 크다면 최대히프, 작다면 최소히프이다.

✏️ Binary Tree 구현 (Python)
Node, Tree class 구현
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def __str__(self):
return str(self.data)
class Tree:
def __init__(self):
self.root = None
순회 구현
* 잠깐! 순회 왜 해야할까?
순회가 필요한 경우는 주로 연결리스트로 트리가 구현되어 있을 경우이다. 트리는 성형구조가 아닌 비선형 구조이기에 모든 노드들을 거쳐가기 위한 방법이 필요한 것이다. 데이터를 삭제할 경우, 서브트리를 삭제하기 위해서는 모든 노드를 거쳐야만 삭제할 수 있기 때문에 순회가 필요하다.
순회의 방법에는 깊이우선탐색(DFS)와 너비우선탐색(BFS)가 있고, 위에서 언급한 전위, 중위, 후위 순회가 DFS이다.
- 중위순회 (inorder)는 이진탐색트리에서 오름차순으로 노드를 얻는데 사용할 수 있다.
- 전위순회 (preorder)는 트리의 복사본을 생성하기 위해 사용하거나, 수식트리에서 prefix 수식을 얻는데 사용할 수 있다
- 후위순회 (postorder)는 트리의 삭제에 이용되고, 수식트리에서 postfix수식을 얻는데 사용된다.
* BFS는 큐를 이용해 구현할 수 있다. 각 레벨의 노드를 큐에 넣고 각 자식의 노드들을 모두 큐에 넣으면서 하나씩 반환하면 된다.
전위순회
def preorder(self, node):
print(node, end='')
if not node.left == None:
self.preorder(node.left)
if not node.right == None:
self.preorder(node.right)D현재노드를 출력 -> L현재노드의 왼쪽 서브트리로 이동 -> R현재노드의 오른쪽 서브트리로 이동
중위순회
def inorder(self, node):
if not node.left == None:
self.inorder(node.left)
print(node, end='')
if not node.right == None:
self.inorder(node.right)L현재노드의 왼쪽 서브트리로 이동 -> D현재노드를 출력 -> R현재노드의 오른쪽 서브트리로 이동
후위순회
def postorder(self, node):
if not node.left == None:
self.postorder(node.left)
if not node.right == None:
self.postorder(node.right)
print(node, end='')L현재노드의 왼쪽 서브트리로 이동 -> R현재노드의 오른쪽 서브트리로 이동 -> D현재노드를 출력
'프로그래밍 > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘] Lower Bound와 Upper Bound (1) | 2022.02.02 |
|---|---|
| Binary Search (이진탐색) 알고리즘 (0) | 2022.02.01 |
| [Python & Algorithm] Dynamic Programming(동적프로그래밍) (0) | 2022.01.22 |
| [Python & Data Structure] Graph (1) | 2021.11.04 |
| [Python & Data Structure] Queue, Stack, Linked List (1) | 2021.11.01 |
![[Python & Data Structure] Tree](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdjELmx%2FbtrjJOUaEyz%2FAAAAAAAAAAAAAAAAAAAAAFKBmhEMP8agNSFnIzXp9YXBGiSnkkQLNGdDujhwgixS%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D5Q87LY6uVA8BHmQRDKPfWYzsmg0%253D)