분류 전체보기

Graph Theory
Suppose that every vertex of a loopless graph G has degree at least 3.Prove that G has a cycle of even length.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 3Solution(i). Let $P = (x_0, x_1, \dots, x_k)$ be a longest path in $G$. Vertices $x_0$ and $x_k$ are the endpoints of $P$.(ii). Since every vertex in $G$ has degree at least 3, $x_0$, being one of the endpoints of $P$, must have at least two neighbors other than $x_1$, which is already on the path. These neighbors must be other verti..
→2024.12.28
Graph Theory
Prove that a graph G is bipartite iff every subgraph H of G has anindependent set consisting of at least half of $V(H)$.
문제출처광주과학기술원-GIST- 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 3SolutionI will show that both directions are true.Necessary condition:If $G$ is bipartite, then every subgraph $H$ of $G$ has an independent set containing at least half of the vertices in $V(H)$.Since $G$ is bipartite, the vertex set $V(G)$ can be divided into two independent sets $A$ and $B$. The subgraph $H$ must have its vertices..
→2024.12.28
Graph Theory
How many simple graphs on n vertices with vertex degrees all even?
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 3SolutionDefine the finite fieldDefine the finite field $F_2$ (with elements 0 and 1). In $F_2$, addition follows modulo 2 arithmetic, meaning $1 + 1 = 0$.Graph setupThe vertex set $V = \{v_1, v_2, \dots, v_n\}$ consists of $n$ vertices.The edge set $E = \{e_1, e_2, \dots, e_m\}$ is the set of all possible edges. The number of edges i..
→2024.12.28
Graph Theory
Prove or disprove: K9 decomposes into copies of C9.
K9의 엣지 개수는 9*(8/2)=36개이고, C9의 엣지개수는 9개이니, 36/9=4로 나누어 떨어져 이론적으로는 4개의 C9 copy로 분해되는게 가능함. 주의할건 이걸로 증명을 마쳐선 안됨. 그 존재성까지 증명해야 증명이 마무리되며, 이는 실제로 보여줌으로써 해결할 수 있음. 본인은 시계방향으로 9개 정점을 0부터 8까지 라벨링하고, 4개의 다른 경로를 가진 C9을 구성함으로써 증명을 해결하였음. 예를 들어,0-1-2-3-4-5-6-7-8-0 으로 1개 발견, 0-2-4-6-8-1-3-5-7-0으로 2개 발견,...이렇게 4개를 찾아보길 바람.
→2024.12.28
Graph Theory
For a simple graph G, prove that G is a cycle iff every vertex has degree 2.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 HomeworkSolutionNecessary condition: If $G$ is a cycle, then every vertex in $G$ has degree 2.(a). A cycle is a simple path that starts and ends at the same vertex. Every vertex is visited exactly once.(b). In a cycle, each vertex is connected to exactly two other vertices: one edge connects to the previous vertex in the cycle, and one edge co..
→2024.12.28
Graph Theory
Use induction to prove that if a graph does not have an odd cycle thenit is bipartite. , Comment: You should first choose which parameter thatyou will apply induction on - number of vertices or number of edges.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2SolutionP(n): A graph with $n$ vertices and no odd cycles is bipartite.(i). Base step:- For $n = 1$, a graph with a single vertex is trivially bipartite.- For $n = 2$, a graph with two vertices cannot have an odd cycle and is bipartite.(ii). Inductive hypothesis:Assume $P(k)$ is true for some positive integer $k$.That is, any graph w..
→2024.12.28
Graph Theory
Prove that the Petersen graph has no cycle of length 7.
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework2Solution(i). Assume that the Petersen graph has a cycle of length 7. Call this cycle ( C_7 ).(ii). Each vertex in ( C_7 ) has two edges within the cycle. Since the Petersen graph is 3-regular, each vertex must have one additional edge connecting to a vertex outside of the cycle.(iii). This additional edge cannot connect to another ver..
→2024.12.28
Graph Theory
Identify the vertices of a Petersen graph in your drawing and explainwhy. (Note again that the vertex set of the Petersen graph is the collec-tion of 2-subsets of [5], for example, 13 means {1, 3}. Two vertices aband cd are adjacent iff {a, b} ∩ {c, d} =∅
문제출처광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2SolutionThe set ([5] = \{1, 2, 3, 4, 5\}) has the following 2-subsets:[12, 13, 14, 15, 23, 24, 25, 34, 35, 45.]These 10 subsets form the 10 vertices of the Peterson graph.To determine adjacency, the rule is:Two vertices (ab) and (cd) are adjacent if and only if (\{a, b\} \cap \{c, d\} =∅).Example:Vertex (34) is adjacent to (12), (25)..
→2024.12.28
Graph Theory
Let Gn be the simple graph with vertex set v0, v1, · · · , vn−1 such that viand vj are adjacent if and only if |j − i| ∈ {4, 5}. Draw the graphs G5 andG6. Determine the number of components of Gn.
문제출처- 광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2Solution(i). G_{5}(ii). G_{6}Number of connected components in $G_{n}$ is $$\begin{cases}n, & \text{if } 0 \leq n \leq 4, \\9 - n, & \text{if } 5 \leq n \leq 8, \\1, & \text{if } n \geq 9.\end{cases}$$
→2024.12.28
Graph Theory
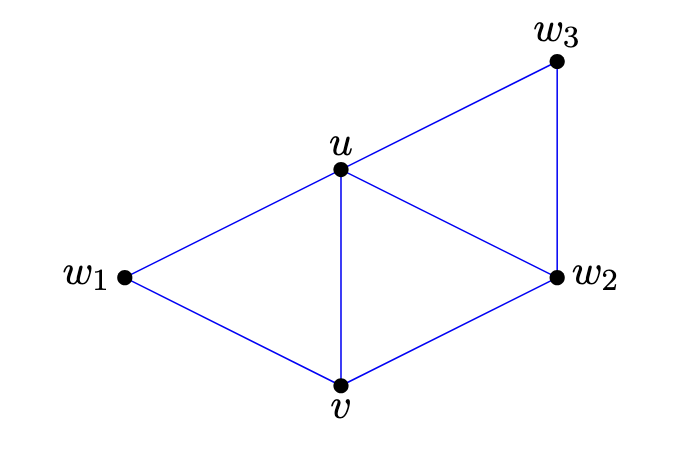
Let u and v be adjacent vertices in a simple graph G. Prove that uvbelongs to at least $$d(u) + d(v) - n(G)$$ triangles in G.
문제출처 - 광주과학기술원(GIST) 최정옥 교수님의 “그래프 이론” 수업, 2024년 가을학기 중 Homework 2Solution(i). Since $u$ and $v$ are adjacent, $uv$ is an edge in $G$.(ii). The number of triangles containing $uv$ is the same as the size of the intersection of $N(u)$ and $N(v)$. $N$ means neighbor.(iii). For example, if $N(u) = \{v, w_1, w_2, w_3\}$ and $N(v) = \{u, w_1, w_2\}$, then: $$N(u) \cap N(v) = \{w_1, w_2\}.$$ Thus, the t..
→2024.12.28

• 이전
• 1
• ···
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• ···
• 28
• 다음