
✏️ 사전정의
지금부터 사용하는 '벡터'라는 단어는 유향성분 벡터가 아닌 벡터공간의 원소를 가리키는 개념으로써 사용한다.
여기서 벡터공간의 field F는 주로 실수집합 R 또는 복소수 집합 C이다.
✏️ vector space
field F에서의 벡터공간(vector space) 또는 선형공간(linear space) V는 다음 8가지 공리를 만족하는 두 연산, 합(sum)과 스칼라 곱(product)를 가지는 집합이다.
(VS1) 모든 x,y ∈ V에 대하여 x+y = y+x 이다. (덧셈의 교환법칙)
(VS2) 모든 x,y,z ∈ V에 대하여 (x+y)+z = x+(y+z) 이다. (덧셈의 결합법칙)
(VS3) 모든 x ∈ V에 대하여 x+0 = 0+x = x 인 0∈V가 존재한다. 이 0을 영벡터(zero vector)라고 부른다.
(VS4) 각 x∈V 마다 x+y=0인 y∈V가 존재한다.
(VS5) 각 x∈V 에 대하여 1x=x이다.
(VS6) 모든 a,b ∈ F와 모든 x∈V에 대하여 (ab)x = a(bx) 이다.
(VS7) 모든 a ∈ F와 모든 x, y∈V에 대하여 a(x+y) = ax+ay 이다.
(VS8) 모든 a,b ∈ F와 모든 x∈V에 대하여 (a+b)x = ax+bx 이다.
✏️ Example
명제의 참과 거짓 판명
(a) 모든 벡터공간에는 영벡터가 있다.
> True. VS3에 따라 모든 x ∈ V에 대하여 x+0 = 0+x = x 인 0∈V가 존재한다. 이 0을 영벡터(zero vector)라고 부른다.
(b) 벡터공간에는 두 개 이상의 영벡터가 있을 수도 있다.> False. Suppose 0과 0'이 벡터공간 V의 두 영벡터라고 해보자.Then, 0+v=v for all v∈V --- (1) 0'+v=v for all v∈V ---(2)equation (1) 에 의해 v=0', 0+0'=0' 이 도출. (3)
equation (2) 에 의해 v=0, 0'+0=0 이 도출. (4)
(3)과 (4)를 이어보면 0=0+0'=0'. 즉 0=0'으로 벡터공간에 zero vector는 unique하다.
(c) 모든 벡터공간에 대하여 ax = bx이면 a=b이다.
> False.
Let x=zero vector.
Then, 1x = 2x. But 1≠2.
(d) 모든 벡터공간에 대하여 ax = ay이면 x=y이다.
> False.
Let a=0.
Then a(1)=a(2), But 1≠2.
(e) F^n에 속한 벡터와 Mnx1(F)에 속한 행렬은 서로 같다고 생각할 수 있다.
> True
F^n의 벡터는 [a11, a21, ..., an1] 이라 할 수 있다. 이 matrix의 크기는 자명하게 nx1이다.
따라서 이것은 Mnx1(F)에 속한 element다.
* field F에서 성분을 가져온 모든 n-tuple의 집합을 F^n이라 표기한다.
(f) mxn 행렬은 m개의 열과 n개의 행으로 이루어져 있다.
> False
matrix의 정의에 의해 m개의 행(row)와 n개의 열(column)로 이뤄져있다.
(g) P(F)에서 다항식의 합은 두 다항식의 차수가 같을 때만 정의한다.
> False.
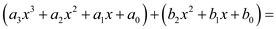
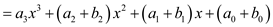
(h) 두 다항식 f와 g의 차수가 n일 때, 다항식 f+g의 차수는 n이다.
> False.
counter example) f(t)=t+1, g(t)=-t. Then f(t)+g(t)=1. 차수가 1에서 0으로 감소했다.
(i) 다항식 f의 차수가 n이고, c가 0이 아닌 스칼라이면 다항식 cf의 차수는 n이다.
> True.
자명하다..?
(j) field F의 0이 아닌 스칼라와 P(F)의 차수가 0인 다항식은 서로 같다고 생각할 수 있다.
> Truescalar a = a·1 = ax^0ax^0이라는 다항식은 차수가 0인 다항식이다.
(k) 함수 f, g ∈ F(S,F) 에 대하여 f=g이기 위한 필요충분 조건은 S의 모든 원소에 대하여 같은 함수값을 가지는 것이다.
> True.
다른 이름으로 정의되었더라도 set F 에서 모든 원소에 대해 같은 함수값을 가지는 두 함수는 똑같이 sum과 product를 가지고 동일하게 동작한다.
아래는 그냥 내가 나중에 참고하려고 붙인 링크
https://zhaouiuc.pages.math.illinois.edu/M416homework/homework1.pdf
'선형대수학' 카테고리의 다른 글
| 5. 기저와 차원 (1) | 2022.02.02 |
|---|---|
| 4. 일차종속과 일차독립 (1) | 2022.02.02 |
| 3. 일차결합(Linear combination)과 Span (0) | 2022.02.02 |
| 2. 부분공간(Subspace) (1) | 2022.02.01 |
